The measles outbreak traced back to Disneyland has spread to eight states, with as many as 95 cases reported by January 28. Media outlets are highlighting the rise of anti-vaccination sentiments. Scientists are expressing their dismay at people who reject sound medical advice, and put their families and communities in harm’s way.
Measles was considered eliminated in the United States in 2000. But if the first month of 2015 is any indication, this year will easily beat the record number of measles cases recorded in 2014.
The narrative during this outbreak, or any measles outbreak really, is that measles is a highly transmissible disease. So transmissible, in fact, that 90 to 95 percent of people must be vaccinated in order to protect the entire population, or achieve what is called herd immunity.
That is partly true. Measles is highly transmissible, not least because people can be contagious days before symptoms develop. But there are three problems with this line of reasoning about vaccination rates.
First, the numbers are based on calculations that assume a world of random mixing. Second, vaccination coverage is not a perfect measure of immunity in the population. Third, and most problematic in my view, is that it gives people a seemingly scientific justification for not getting vaccinated—after all, if not everyone needs to get vaccinated in order to attain herd immunity, can it really be so bad if I opt out of it?
What exactly is herd immunity?
Let’s look at the concept of herd immunity first. The basic idea is that a group (the “herd”) can avoid exposure to a disease by ensuring that enough people are immune, so that no sustained chains of transmission can be established. This protects an entire population, especially those who are too young or too sick to be vaccinated. But how many people need to be immune to achieve this?
In order to calculate the number of people who need to be immune for herd immunity to be effective, we need to know how many people will get infected, on average, by an infectious person.
Imagine that a newly infected person will on average pass on the disease to two other people. Those two will each infect another two people, who will themselves pass it on, and so on, resulting in the classical pattern of an exponentially growing outbreak.
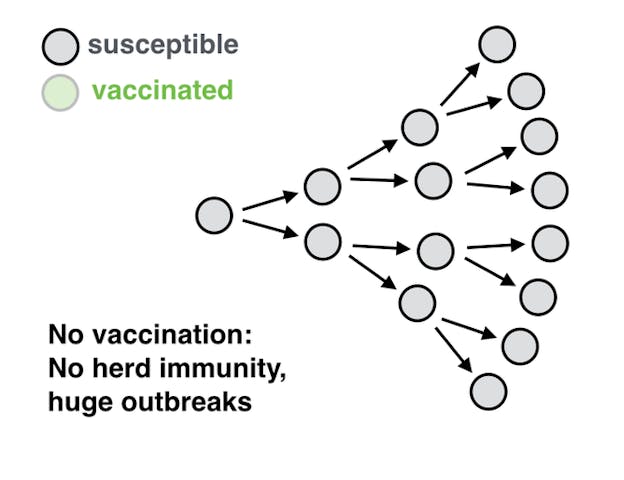
In order to stop the growth in the number of transmissions, we need to ensure that each individual case causes, on average, less than one new infection. So, let’s say that one case leads on average to two more infections, but instead we want that number to be less than one. That means at least 50 percent of the population needs to be immune, so that at most only one of the two people who might have been infected by an individual will be.
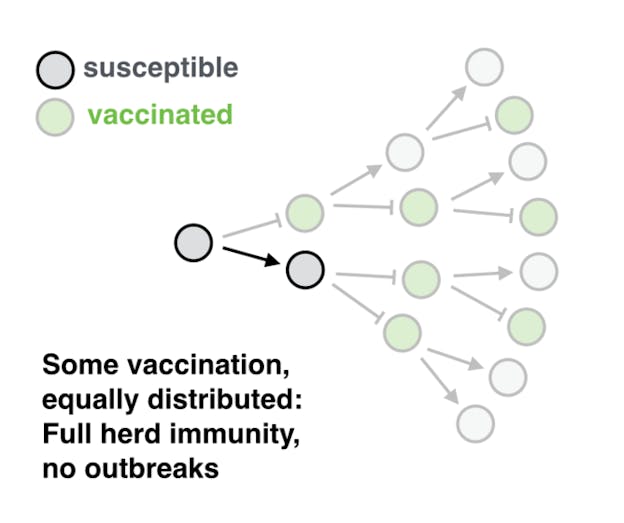
How many people need to get vaccinated to achieve herd immunity?
So, how do we calculate what fraction of a population needs to be immune to reach herd immunity? First, we need to know what the reproduction number, or R, is. That’s how many new cases a single case of an infection will cause.
Imagine that you are infected in a completely susceptible population, and you pass on the infection to five other people (ie R=5). In order to prevent an outbreak, at least four out of those five people, or 80 percent of the population in general, should be immune. Put differently, 20 percent of the population may remain individually susceptible, but the population would still remain protected.
So if you can estimate the reproduction number for a given disease, you can calculate the fraction of the population that needs to be immune in order to attain herd immunity.
For influenza and Ebola, the number R is about two. For polio and smallpox, it is around five to eight. But for measles it is much higher, somewhere between ten and 20. And because of that, the goal for measles vaccination coverage is typically around 90 to 95 percent of a population.
But there’s a problem with this calculation.
The population is not random
The assumption underlying the calculation for herd immunity is that people are mixing randomly, and that vaccination is distributed equally among the population. But that is not true. As the Disneyland measles outbreak has demonstrated, there are communities whose members are much more likely to refuse vaccination than others.
Geographically, vaccination coverage is highly variable on the level of states, counties, and even schools. We’re fairly certain that opinions and sentiments about vaccination can spread in communities, which may in turn lead to polarized communities with respect to vaccination.
And media messages, especially from social media, may make the problem worse. When we analyzed data from Twitter about sentiments on the influenza H1N1 vaccine during the swine flu pandemic in 2009, we found that negative sentiments were more contagious than positive sentiments, and that positive messages may even have back-fired, triggering more negative responses.
And in measles outbreak after measles outbreak, we find that the vast majority of cases occurred in communities that had vaccination coverages that were way below average.
The sad truth is this: As long as there are communities that harbor strong negative views about vaccination, there will be outbreaks of vaccine-preventable diseases in those communities. These outbreaks will happen even if the population as a whole has achieved the vaccination coverage considered sufficient for herd immunity.

If negative vaccination sentiments become more popular in the rest of the population as well, we may start to see more sustained transmission chains. Once those chains are sufficiently frequent to connect under-vaccinated communities, we may again be in a situation of endemic measles.
The solution often proposed is that we should do a better job of convincing people that vaccines are safe. I’m all for it. But I would also suggest that we should stop basing our vaccination policies on models that made sense in a world of constrained vaccine supply, and aim for 100 percent vaccination coverage among those who can get vaccinated.
This would also solve another problem, often glanced over: There are many people who cannot get vaccinated for medical reasons, either because they are too young or because they have other conditions that prevent them from acquiring immunity through vaccination.
Herd immunity against measles requires that 90 to 95 percent of the entire population are immune, whereas vaccination coverage is measured as the percentage vaccinated of the target population—which only includes people who are eligible for vaccination. This means that to achieve 95 percent immunity in the population for measles, vaccination coverage needs to be higher than 95 percent. This is the scientific argument for a public health policy that aims at 100 percent vaccination coverage.
More importantly, there is an ethical argument to be made for the goal of 100 percent vaccination coverage. It sends the right message. Everyone who can get vaccinated, should get vaccinated—not only to protect themselves, but to protect those who can’t, through herd immunity.
![]()
This article was originally published on The Conversation. Read the original article.
